
Üslü İfadeler Konu Anlatım Videosu-1
Üslü İfadeler Konu Anlatım Videosu -2
Üslü İfadeler Konu Anlatım Videosu -3
Üslü İfadeler Konu Anlatım Videosu -4
ÜSLÜ İFADELER
a bir tam sayı, n bir doğal sayı olmak üzere n tane a’nın çarpımı, şeklinde gösterilir.
Üslü İfadeler İle İlgili Bazı Kurallar
*Sıfırdan farklı bir tam sayının sıfırıncı kuvveti daima 1’dir.
Örnek:
*Üssü 1 olan sayılar kendisine eşittir.
Örnek:
*Pozitif tam sayıların çift ve tek üstlerinde sonuç pozitiftir.
Örnek:
Negatif tam sayıların çift üstlerinde sonuç pozitif tek üstlerinde negatiftir.
(Çift üslerinde pozitif olması için üs ile taban arasında parantez olmalıdır.)
Örnek:
*Üs (-) ise bu çarpanlara göre tersi anlamındadır. Tabandaki sayının çarpmaya göre tersi alındıktan sonra üssü alınır.
Örnek:
Örnek:
(Bu örnekte az önce yaptığımız işlemin tersini düşünmeliyiz. 6 sayısı paydadan paya geçerken üssü negatif değer aldı.)
*Üssün üssü çarpılır
Örnek:




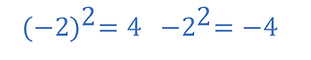




Üslü İfadeler İle ÇARPMA-BÖLME
1)ÇARPMA
Üslü ifadelerle çarpma işlemi yapılırken eğer;
>Tabanlar aynı üsler farklı ise sonuçta taban aynen yazılır, üsler toplanır.
Örnek:
>Tabanlar farklı üsler aynı ise sonuçta tabanlar çarpılır, üstler aynen kalır.
Örnek:




2)Bölme
Üslü ifadelerle bölme işlemi yapılırken eğer;
>Tabanlar aynı, üsler farklı ise sonuçta üsler çıkarılır, taban aynen yazılır.
Örnek:
Not: Eğer çıkarılması gereken üs negatif tam sayı ise işaret değiştirmesi gerektiğini unutmamalıyız.
Örnek
>Tabanlar farklı, üsler aynı ise sonuçta tabanlar bölünür, üsler aynı kalır.
Örnek:
Not: Bölmede ve çarpmada eğer hem tabanlar eşit hem de üsler eşitse tabanlar aynen kalır üstler arasında işlemler yapılır.
Örnek:
Örnek:
Bölmede ve çarpmada eğer hem tabanlar hem de üsler eşit değilse tabanlar en küçük tabana benzetilerek işlem yapılır.
Örnek:
Çözüm:




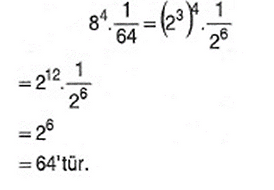
10’un Pozitif ve Negatif Tam Sayı Kuvvetleri ve Bilimsel Gösterimler
-
10’un Pozitif ve Negatif Tam Sayı Kuvvetleri
>Pozitif Kuvvetleri
Örnek:
>Negatif Kuvvetleri
Örnek:
>10’un Kuvvetleri İle Çözümleme
Örnek:
268,174 sayısını 10’un kuvvetleri şeklinde çözümleyelim.
Çözüm:
Not: Ondalık sayıları 10’un kuvvetleri şeklinde gösterirken virgül (,) sola kaydırılırsa 10’un üzerindeki kuvvet artar.
Sağa kaydırılırsa 10’un üzerindeki kuvvet azalır.
Örnek:







2.Bilimsel Gösterimler
Sayı 10’dan küçük ve 1 den büyük veya eşit olacak şekilde 10’un kuvvetleri ile yazılır.
1 ≤ sayı < 10
Örnek:
369 sayısının bilimsel gösterimini bulalım,
Çözüm:
369 sayısı 1’e eşit veya 1’den büyük; 10’dan küçük olacak şekilde göstermek için 3,69 şeklinde yazılır.
Örnek:

Yukarıda bazı varlıkların ağırlıkları ve ağırlıklarının bilimsel gösterimleri verilmiştir.
Buna göre, hangi varlığın ağırlığının bilimsel gösterimi yanlış yazılmıştır?
Çözüm:


