ÜÇGENİN YARDIMCI ELEMANLARI
-
Yükseklik
Üçgenin bir köşesinden karşısındaki kenara veya uzantısına çizilen dik doğru parçasına o kenara ait yükseklik denir.
>Yükseklikler dar açılı üçgenlerde üçgenin içerisindeki bir noktada kesişir.
>Geniş açılı üçgende yüksekliklerin uzantıları üçgenin dışındaki bir noktada kesişir.
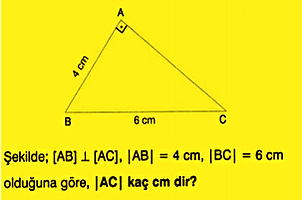
>Bir dik üçgende dik kenarlar aynı zamanda yüksekliktir
Örnek:
Çözüm:
2. Açıortay
Üçgenin bir köşesindeki açıyı iki eş parçaya ayıran doğru parçasına açıortay denir.
Açıortaylar üçgen içerisinde bir noktada kesişir.
Şekildeki ABC üçgeninin;
-
A açısına ait açıortayı [AE]’dır.
-
B açısına ait açıortayı [BF]’dır.
-
C açısına ait açıortayı [CD]’dır
ABC üçgeninde açıortaylar K noktasında kesişmektedir.
Bir üçgende açıortaylar, üçgenin içinde kesişir.
Örnek:
Çözüm:
3.Kenarortay
Üçgenin bir köşesinden karşı kenarın orta noktasını birleştiren (kenarı ortadan bölen) doğru parçasına o kenara ait kenarortay denir. Kenarortaylar üçgen içerisinde bir noktada kesişir.
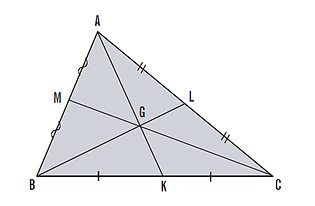
Şekildeki ABC üçgeninin;
-
BC kenarına ait kenarortayı [AK]’dır.
-
AC kenarına ait kenarortayı [BL]’dır.
-
AB kenarına ait kenarortayı [CM]’dır.
ABC üçgeninde kenarortaylar G noktasında kesişmektedir.
Bir üçgendeki kenarortaylar, üçgenin içinde kesişir.
Not: Üçgenin kenarortaylarının kesim noktasına, üçgenin ağırlık merkezi denir. Üçgensel bölge şeklindeki bir nesnenin ağırlık merkezi, bu nesnenin denge noktasıdır. Yukarıdaki ABC üçgenin denge noktası (ağırlık merkezi) G noktasıdır.
4.Kenar Orta Dikme
Üçgenin kenarlarını dik olarak iki eş parçaya bölen doğrulara kenar orta dikmeleri denir.
Şekildeki ABC üçgeninin;
• BC kenarının kenar orta dikmesi d doğrusudur.
• AC kenarının kenar orta dikmesi e doğrusudur.
• AB kenarının kenar orta dikmesi f doğrusudur.













ÜÇGEN EŞİTSİZLİĞİ
Bir üçgende uzunlukları arasında; bir uzunluk diğer uzunlukların toplamından küçük, farklarının mutlak değerinden ise büyük olmak zorundadır.
Yukarıdaki üçgenin a kenarı için üçgen eşitsizliği |b – c| < a < b + c şeklinde yazılır.
c kenarı için,
|b – a| < c < b + a
b kenarı için,
|a – c| < b < a + c şeklinde yazılır.
Örnek:
Çözüm:
NOT: Üçgenlerde büyük açı karşısına büyük kenar, küçük açı karşısına kısa kenar gelir.
IACI > IABI > IBCI
Örnek:
Çözüm:
Önce ABC üçgeninde, sonra ACD üçgeninde
|AC| için üçgen eşitsizliğini yazalım.
||BC| – |AB|| < |AC| < |BC| + |AB|
8 – 5 < |AC| < 8 + 5
3 < |AC| < 13
||CD| – |AD|| < |AC| < |CD| + |AD|
11 – 6 < |AC| < 11 + 6
5 < |AC| < 17
Elde edilen 3 < |AC| < 13 ve 5 < |AC| < 17 eşitsizlikleri birleştirilirse, 5 < |AC| < 13 olur.
Bu durumda |AC| nin en küçük tam sayı değeri 6, en büyük tam sayı değeri 12 olur.
Bir Üçgenin Belirli Olabilme Şartları
-
Kenar-Açı-Kenar
İki kenarı ve bu iki kenar arasındaki açısı bilinen üçgenler çizilebilir.
[AB], [BC] uzunlukları ve m(ABC) açısı bilinen bir tek ABC üçgeni çizilebilir.
2.Kenar-Kenar-Kenar
Üç kenarı bilinen üçgenler.
[AB], [AC] ve [BC] uzunlukları biliniyor ve üçgen eşitsizliğini sağlıyorsa bir tek ABC üçgeni çizilebilir.
3.Kenar-Kenar-Kenar
Bir kenarı ve bu kenarın oluşturduğu köşelerdeki açıları bilinen üçgenler.
[AB], m(BAC) açısı ve m(ABC) açısı biliniyorsa bir tek ABC üçgeni çizilebilir.
Örnek:
Aşağıda kenar ve açı değerleri verilen üçgenlerden hangileriyle sadece bir tane üçgen çizilebilir?
-
s(A) = 90°, s(B) = 40° ve s(C) = 50° olan ABC
-
|KL| = 5 cm, |LM| = 7 cm ve s(KLM)= 90° olan KLM
-
s(P) = 50°, s(R) = 40° ve |PR| = 10 cm olan PRS
Çözüm: I için, üç açısı bilinen üçgenlerle birden çok üçgen çizilebilir. II, iki kenarı ve bu kenarlar arasındaki açı bilindiği için sadece tek bir üçgen çizilebilir. III için, iki açısı ve bir kenarı (karşısındaki açısı bilinmeyen) bilinen sadece bir üçgen çizilebilir.
II ve III’te verilen değerlerle sadece bir üçgen çizilebilir.





Pisagor Bağıntısı
Bir dik üçgende, dik kenarların uzunluklarının karelerinin toplamı hipotenüsün (dik açının karşısındaki kenarın) karesine eşittir.
Örnek:
Çözüm:
NOT: Kenarları tam sayılardan oluşan dik üçgenlerin bilinmesin bize birçok sorunu pratiklik kazandırır kenarları tam sayı olan üçgenlerden en çok kullanılanları şunlardır;
> 3-4-5 üçgeni
(bu üçgenlerin katları ile de karşılaşabilirsiniz. 2 katı 6-8-10, 3 katı 9-12-15 gibi…)
> 5-12-13 üçgeni
> 8-15-17 üçgeni
> 7-24-25 üçgeni
Örnek:
Çözüm:
NOT: İkizkenar dik üçgenlerde Pisagor bağıntısı a-a-a√2 olarak kolaylıkla bulunur.