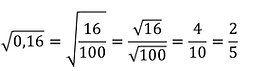Kareköklü İfadeler Konu Anlatım Videosu-1
Kareköklü İfadeler Konu Anlatım Videosu -2
Kareköklü İfadeler Konu Anlatım Videosu-3
Kareköklü İfadeler Konu Anlatım Videosu -4
Kareköklü İfadeler Konu Anlatım Videosu-5
Kareköklü İfadeler Konu Anlatım Videosu -6
Tam Kare Doğal Sayılar
Bir doğal sayının karesi tam kare doğal sayıdır.
>Karenin alanı tam karedir.
Tam Kare Doğal Sayıların Karekök İlişkileri
>Verilen bir sayının Hangi sayının karesi olduğunu bulma işlemine karekök alma denir.
>Alanı bilinen bir karenin bir kenarının uzunluğu alanının karekökü ile bulunur.
> √ sembolü ile gösterilir.
>Bir sayının karekökü hiçbir zaman negatif olamaz.



Kareköklü İfadeler
-Tam Kare Doğal Sayılar
-Tam Kare Olmayan Sayıların Hangi İki Sayı Arasında Olduğunu Bulma
-Gerçek Sayılar
Tam Kare Olmayan Sayıların Hangi İki Doğal Sayı Arasında Olduğunu Belirleme
Tam kare olmayan sayıların karekökleri iki ardışık doğal sayı arasındadır.
Örnek:
sayısı hangi iki doğal sayı arasındadır?
Örnek:
Çözüm:
İlk olarak 35 sayısından bir küçük bir de büyük tam kare doğal sayılar bulunur. 25 ve 36’dır. Bu durumda,
5 ile 6 sayıları arasındadır. B noktasına en yakındır.


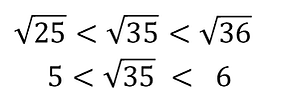
Gerçek Sayılar
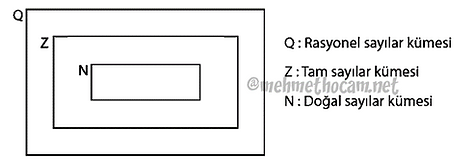
Doğal sayıların N, tam sayıların Z ve rasyonel sayıların da Q ile gösterildiğini öğrenmiştik.
Bu sayı kümeleri arasında, N ⊂ Z ⊂ Q şeklinde alt küme ilişkisi vardır. Yani her doğal sayının bir tam sayı olduğunu, her tam sayının da bir rasyonel sayı olduğunu biliyoruz. Rasyonel sayılar kümesi, tam sayılar kümesini; tam sayılar kümesi de doğal sayılar kümesini kapsamaktadır.
İrrasyonel Sayılar
a, b tam sayı ve b ≠ 0 olmak üzere, bir sayı şeklinde yazılmıyorsa bu sayı rasyonel değildir. Bu tür sayılara rasyonel olmayan anlamında irrasyonel sayılar denir.
Karekök dışına çıkmayan köklü sayılar birer irrasyonel sayıdır.
Örneğin
*π (pi) sayısının gerçek değeri 3,14 değildir. Bu işlem kolaylığı için yaklaşık olarak alınan değerdir. π sayısında virgülden sonraki bir milyonuncu basamağa kadar bilgisayar yardımıyla ulaşıldı ve devirli ondalık sayı olmadığı görüldü. Yani π sayısı rasyonel sayı değildir.
* NOT : Devirli ondalık sayılar şeklinde yazılabildikleri için rasyonel sayılar kümesine ait sayılardır.
Örnek:
Çözüm:
*Artık rasyonel olmayan sayılara irrasyonel sayılar dendiğini biliyoruz. İrrasyonel sayılar kümesi “I” harfi ile gösterilir.
*İrrasyonel sayılar kümesi ile rasyonel sayılar kümesinin birleşimi gerçek(reel) sayılar kümesini oluşturur ve bu küme R harfi ile gösterilir.
8.SINIF Konu anlatım ve soru çözüm videolarımız için Youtube kanalımız Mehmet HOCA'yı ziyaret edebilirsiniz…



Kareköklü İfadelerde Çarpma İşlemi
Kareköklü sayılarda çarpma işleminde kat sayılar kendi aralarında, karekök içindeki sayılar da kendi aralarında çarpılır.
Örnek:
Not: Eğer karekök önünde kat sayı yoksa 1 ile çarpılır.
Örnek:
Örnek: Aşağıdaki şekilde kenar uzunlukları verilmiş olan dikdörtgenin alanını bulalım.
Çözüm: Dikdörtgenin alanı uzun kenar ile kısa kenarın çarpımına eşittir.
Kareköklü İfadelerde Bölme İşlemi
Kareköklü sayılarla bölme işlemi yapılırken kat sayılar kendi aralarında, karekök içindeki sayılar da kendi aralarında bölünür.
Örnek:
Örnek: Alanı ve bir kenarının uzunluğu verilen aşağıdaki dikdörtgenin diğer kenarının uzunluğu kaçtır?
Çözüm: Dikdörtgenin alanı uzun kenar ile kısa kenarın çarpımına eşit olduğu için alanı , uzunluğu bilinen kenara bölerek diğer kenarın uzunluğunu bulabilirz.
8.SINIF Konu anlatım ve soru çözüm videolarımız için Youtube kanalımız Mehmet HOCA'yı ziyaret edebilirsiniz…



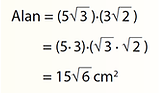
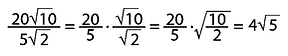


1. Kareköklü İfadeleri a√b Şeklinde Yazma
Kareköklü bir sayıyı a√b şeklinde yazmak için karekök içindeki sayı çarpanlarından en az biri tam kare sayı olacak şekilde iki sayının çarpımı olarak yazılır. Tam kare olan çarpanların karekökleri, karekök dışına katsayı olarak yazılır.
Örnek: √20 sayısını a√b şeklinde yazalım.
Çözüm: Bunun için ilk olarak 20 sayısının asal çarpanlarını buluruz.
20= 2. 2. 5 = 4.5
√20 = √4 . √5 => 4 kökten dışarıya 2 olarak çıkabileceği için sonuçta √20 = 2√5 olarak bulunur.
Örnek: Alanı 98 santimetrekare olan karenin bir kenar uzunluğunu bulalım.
Çözüm: Alanı 98 santimetrekare olan karenin bir kenar uzunluğu 98 cm olur. 98 sayısını asal çarpanlarına ayıralım.
Karenin bir kenar uzunluğu √98 = 7√2
Örnek:
Çözüm: 10800 sayısını asal çarpanlarına ayıralım.
2. Kareköklü Sayılarda Katsayıyı Kök İçine Alma
Katsayı karekök içine alınırken katsayının karesi alındıktan sonra kök içindeki sayı ile çarpılır en sonunda da kök içine yazılır.
Örnek: 3√5 şeklinde verilen sayıda 3’ü kök içine alalım.
Çözüm:
Örnek:
ifadesinde a’nın değeri kaçtır? aşağıdakilerden hangisine eşittir?
Çözüm:




Kareköklü İfadelerde Toplama Çıkarma
Kareköklü sayılarla toplama ve çıkarma işlemi yaparken, kök içleri aynı olan terimler kendi aralarında toplanır veya çıkarılır. Katsayılar arasında işlem yapılır ve bulunan sonuç ortak kökte katsayı olarak yazılır.
Not: Kök içleri aynı olmayan ifadelerle toplama ve çıkarma işlemi yapılmaz.
Örnek:
İşleminin sonucu kaçtır?
Çözüm:
Örnek: Aşağıdakilerden hangisi √12 ile toplanırsa sonuç √48 olur?
Çözüm:
Örnek:
Çözüm:
Örnek:
Çözüm:



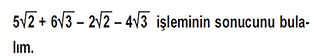


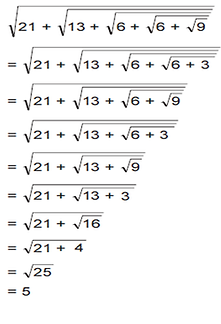
Ondalık İfadelerin Karekökü
Ondalık ifadelerin karekökü bulunurken ondalık kesir rasyonel olarak yazılır ve pay ile payda ayrı ayrı kökten çıkarılır.
Örnek: İfadesinin değeri kaçtır?
Çözüm:
Örnek: İfadesinin değeri kaçtır?
Çözüm:
Örnek: İfadesinin değeri kaçtır?
Çözüm:
Örnek:
Çözüm: